5.5.2 Finding Mean and Standard Deviation

In this topic we will learn how to

solve problems concerning a variable $X$ , where $X \sim N(\mu, \sigma^{2})$ , including finding a relationship between $x_{1}$ , $\mu$ and $\sigma$ given the value of $P(X > x_{1})$ or a related probability

There are questions where you will be asked to evaluate $\mu$ , $\sigma$ or both. In those questions, you have to use the given information to find the unknown(s).

Let’s walk through some past paper questions to better understand this idea.

1. The weights of bags of sugar are normally distributed with mean $1.04$ kg and standard deviation $\sigma$ kg. In a random sample of $2\ 000$ bags of sugar, $72$ weighed more than $1.10$ kg. Find the value of $\sigma$ . (9709/52/M/J/21 number 2)

Define the random variable,
$X\textmd{ - r.v, weights, in kg, of bags of sugar}$ State the distribution and parameters of the random variable,
$X \sim N(1.04, \sigma^{2})$ Let’s write out, mathematically, the information we have been given in the question,
$P(X > 1.10) = \frac{72}{2\ 000}$ We can use this to find $\sigma$ . Let’s simplify,
$P(X > 1.10) = 0.036$ Let’s standardize,
$P\left(Z > \frac{1.10 - 1.04}{\sigma}\right) = 0.036$ Let’s replace $\frac{1.10 - 1.04}{\sigma}$ with $z$ for better readability,
$P(Z > z) = 0.036$

Rendered by QuickLaTeX.com

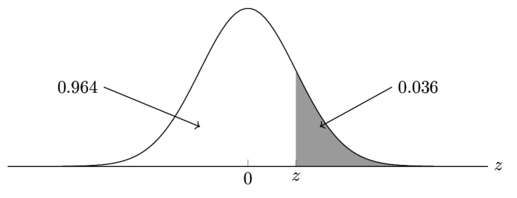
From the diagram, we can tell that $z$ is going to be positive. Since $0.036$ is less than $0.500$ let’s subtract it from $1$ ,
$1 - 0.036 = 0.964$ Let’s use the tables in reverse to find $z$ ,
$z = \phi^{-1}{\left(0.964\right)}$ $z = 1.798$ Note: The notation $\phi^{-1}{(a)}$ means we’re using the tables in reverse.

Now that we have found $z$ , we can find $\sigma$ ,
$z = \frac{1.10 - 1.04}{\sigma}$ $1.798 = \frac{0.06}{\sigma}$ $\sigma = \frac{0.06}{1.798}$ $\sigma = 0.03337041157$ Give your answer correct to $3$ significant figures,
$\sigma = 0.0334$ Therefore, the final answer is,
$\sigma = 0.0334$ 2. The systolic blood pressure (SBP) of $12$ -year old children is normally distributed with mean $117$ . Of these children $88\%$ have SBP more than $108$ . (9709/51/O/N/22 number 4)

Define the random variable,
$X \textmd{- r.v, SBP of }12\textmd{-year-old children}$ State the distribution and parameters of the random variable,
$X \sim N(117, \sigma^{2})$ Let’s write out, mathematically, the information we have been given in the question,
$P(X > 108) = 0.88$ Let’s standardize,
$P\left(Z > \frac{108 - 117}{\sigma}\right) = 0.88$ Let’s replace $\frac{108 - 117}{\sigma}$ with $z$ for better readability,
$P(Z > z) = 0.88$

Rendered by QuickLaTeX.com

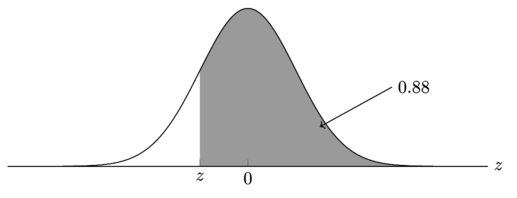
From the diagram, we can tell that $z$ is going to be negative.

Let’s use the tables in reverse to find $z$ ,
$z = \phi^{-1}{(0.88)}$ $z = 1.175$ Remember that our $z$ -value is supposed to be negative,
$z = -1.175$ Now that we have found $z$ , we can find $\sigma$ ,
$z = \frac{108 - 117}{\sigma}$ $-1.175 = \frac{108 - 117}{\sigma}$ $\sigma = \frac{-9}{-1.175}$ $\sigma = 7.659574468$ Give your answer correct to $3$ significant figures,
$\sigma = 7.66$ Therefore, the final answer is,
$\sigma = 7.66$ 3. The lengths of the leaves of a particular type of tree are modelled by a normal distribution. A scientist measures the lengths of a random sample of $500$ leaves from this type of tree and finds that $42$ are less than $4$ cm long and $100$ are more than $10$ cm long. Find estimates for the mean and standard standard deviation of the lengths of the leaves from this type of tree. (9709/53/M/J/21 number 5)

Define the random variable,
$X \textmd{- r.v, lengths, in cm, of leaves of a particular type of tree}$ State the distribution and parameters of the random variable,
$X \sim N(\mu, \sigma^{2})$ Let’s write out, mathematically, the information we have been given in the question,
$P(X < 4) = \frac{42}{500}\ \ \ \ \ \ P(X > 10) = \frac{100}{500}$ We can use this information to form two simultaneous equations, in terms of $\mu$ and $\sigma$ . Let’s simplify,
$P(X < 4) = 0.084\ \ \ \ \ \ P(X > 10) = 0.20$ Let’s standardize,
$P\left(Z < \frac{4 - \mu}{\sigma}\right) = 0.084\ \ \ \ \ \ P\left(Z > \frac{10 - \mu}{\sigma}\right) = 0.20$ Let’s substitute $\frac{4 - \mu}{\sigma}$ and $\frac{10 - \mu}{\sigma}$ , with $z_{1}$ and $z_{2}$ respectively for better readability,
$P(Z < z_{1}) = 0.084\ \ \ \ \ \ P(Z > z_{2}) = 0.20$

Rendered by QuickLaTeX.com

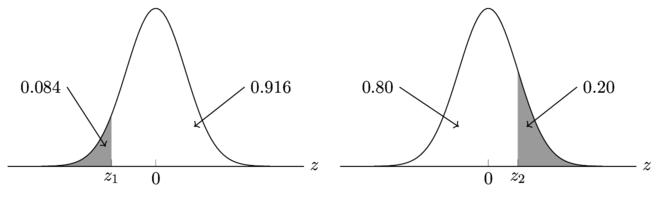
From the diagrams, we can tell that $z_{1}$ is going to be negative and $z_{2}$ is going to be positive.

Let’s use the tables in reverse to find $z$ ,
$z_{1} = \phi^{-1}{(0.916)}\ \ \ \ \ \ z_{2} = \phi^{-1}{(0.80)}$ $z_{1} = 1.378\ \ \ \ \ \ z_{2} = 0.842$ Remember that $z_{1}$ is supposed to be negative,
$z_{1} = -1.378\ \ \ \ \ \ z_{2} = 0.842$ Now let’s go back to the expressions for $z_{1}$ and $z_{2}$ from earlier,
$z_{1} = \frac{4 - \mu}{\sigma}\ \ \ \ \ \ z_{2} = \frac{10 - \mu}{\sigma}$ Substitute $z_{1}$ and $z_{2}$ respectively,
$-1.378 = \frac{4 - \mu}{\sigma}\ \ \ \ \ \ 0.842 = \frac{10 - \mu}{\sigma}$ Make both equations linear,
$-1.378\sigma = 4 - \mu \ \ \ \ \ \ \ \ 0.842\sigma = 10 - \mu$ Now solve the two equations simultaneously, to evaluate both $\mu$ and $\sigma$ ,
$-1.378\sigma = 4 - \mu \ \ \ \ \ \ \ \ 0.842\sigma = 10 - \mu$ $\mu = 4 + 1.378\sigma$ $0.842\sigma = 10 - \mu$ $0.842\sigma = 10 - (4 + 1.378\sigma)$ $0.842\sigma = 10 - 4 - 1.378\sigma$ $0.842\sigma = 6 - 1.378\sigma$ $0.842\sigma + 1.378\sigma = 6$ $2.22\sigma = 6$ $\sigma = 2.702702703$ $\mu = 4 + 1.378\sigma$ $\mu = 4 + 1.378(2.702702703)$ $\mu = 7.724324324$ Give your answers correct to $3$ significant figures,
$\sigma = 2.70 \ \ \ \ \mu = 7.72$ Therefore, the final answer is,
$\sigma = 2.70 \ \ \ \ \mu = 7.72$