1.2.3 Transformations - GCEALevelMaths9709

In this topic we will learn how to:

understand and use transformations of the graph of $y = f(x)$ given by, $y = f(x) + a$ , $y = f(x + a)$ , $y = af(x)$ , $y = f(ax)$ and simple combinations of these.

$\textbf{\Large\textcolor{gray}{Transformations}}$

$\textbf{\textcolor{gray}{y = f(x) + a}}$ This is a translation in the y-axis by $a$ units.
Here’s an example of what that would look like graphically.

Example 1
Given that $f(x) = x^{2}$ sketch the graph of $g(x) = f(x) + 2$ .

Rendered by QuickLaTeX.com

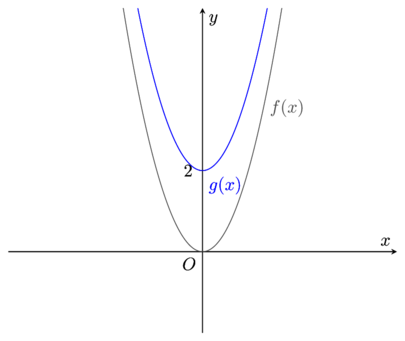
$\textbf{\textcolor{gray}{y = f(x + a)}}$ This is a translation in the x-axis by $-a$ units.
Here’s an example of what that would look like graphically.

Example 2
Given that $f(x) = x^{2}$ sketch the graph of $g(x) = f(x + 2)$ .

Rendered by QuickLaTeX.com

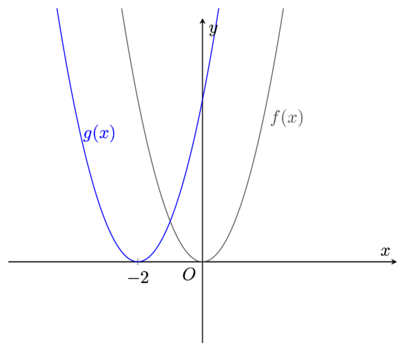
$\textbf{\textcolor{gray}{y = af(x)}}$ This is a stretch in the y-axis by a stretch factor of $a$ .
Here’s an example of what that would look like graphically.

Example 3
Given that $f(x) = x^{2}$ sketch the graph $g(x) = 2f(x)$ .

Rendered by QuickLaTeX.com

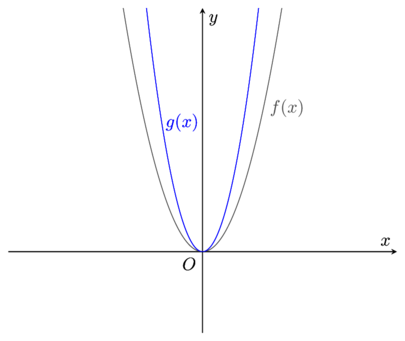
$\textbf{\textcolor{gray}{y = f(ax)}}$ This is a stretch in the x-axis by a stretch factor of $\frac{1}{a}$ .
Here’s an example of what that would look like graphically.

Example 4
Given that $f(x) = (x - 2)^{2}$ sketch the graph $g(x) = f(2x)$ .

Rendered by QuickLaTeX.com

$\textbf{\large\textcolor{gray}{Combined Transformations}}$ $\textcolor{gray}{a(bx + c)^{2} + d}$ The above is an example of a combined transformation. $a$ represents a stretch in the y-axis. $b$ represents a stretch in the x-axis. $c$ represents a translation in the x-axis. $d$ represents a translation in the y-axis.
Here’s an example of a combined transformation.

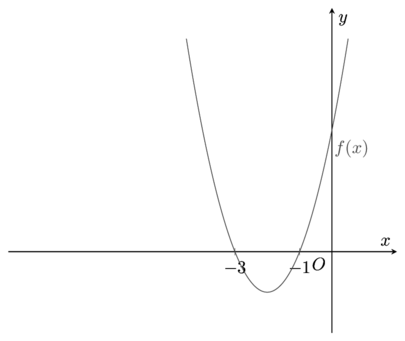
Example 5
Given that $f(x) = (x + 2)^{2} - 1$ sketch the graph $g(x) = 3f(2x + 4) + 1$ .

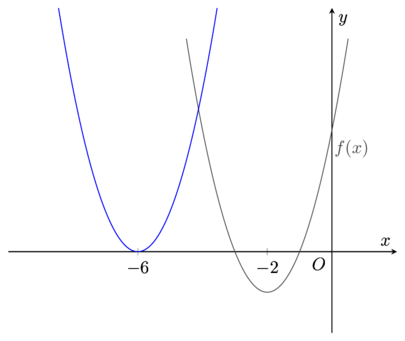
Start by sketching the graph of $y = f(x)$ ,

Rendered by QuickLaTeX.com

$g(x) = 3f(2x + 4) + 1$ From $f(x)$ to $g(x)$ there is a translation in the $x$ -direction by $-4$ units and a translation in the $y$ -direction by $1$ unit. Let’s translate $f(x)$ by $-4$ units in the $x$ -direction and $1$ unit in the $y$ -direction,

Rendered by QuickLaTeX.com

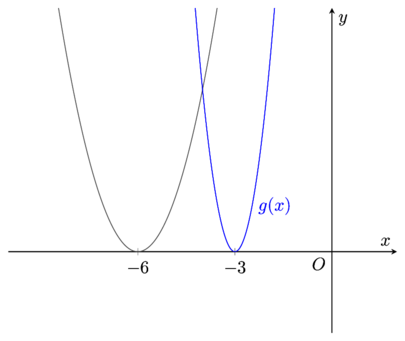
$g(x) = 3f(2x + 4) + 1$ Finally, there is a stretch in the $x$ -direction by a stretch factor of $\frac{1}{2}$ and a stretch in the $y$ -direction by a stretch factor of $3$ ,

Rendered by QuickLaTeX.com

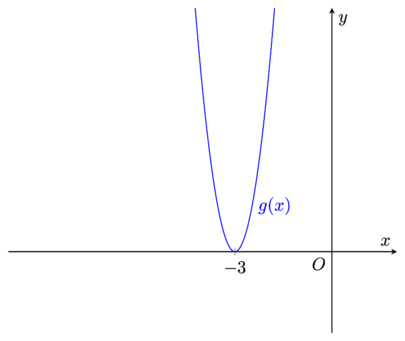
Therefore, the graph of $y = g(x)$ is,

Rendered by QuickLaTeX.com

Let’s look at some past paper questions.

1. The graph of $y = f(x)$ is transformed to the graph $y = 1 + f\left(\frac{1}{2}x\right)$ . Describe fully the transformations which have been combined to give the resulting transformation. (9709/12/F/M/20 number 2)

Start by describing the transformation in the x-axis,
There is a stretch in the x-direction by a stretch factor of $2$ .

Then describe the transformation in the y-axis,
There is a translation in the y-direction by $1$ unit.

Therefore, the final answer is,
There is a stretch in the x-direction by a stretch factor of $2$ . Followed by a translation in the y-direction by $1$ unit.

2. The graph of $y = f(x)$ is transformed to the graph $y = 2f(x - 1)$ . Describe fully the two single transformations which have been combined to give the resulting transformation. (9709/12/M/J/21 number 2)

Start by describing the transformation in the x-axis,
There is a translation in the x-direction by $1$ unit.

Then describe the transformation in the y-axis,
There is a stretch in the y-direction by a stretch factor of $2$ .

Therefore, the final answer is,
There is a translation in the x-direction by $1$ unit. Followed by a stretch in the y-direction by a stretch factor of $2$

3. Functions $f$ and $g$ are both defined for $x \in \mathbb{R}$ and are given by

$f(x) = x^{2} - 2x + 5$
$g(x) = x^{2} + 4x + 13$

(9709/13/M/J/21 number 6)

(a) By first expressing each of $f(x)$ and $g(x)$ in completed square form, express $g(x)$ in the form $f(x + p) + q$ , where $p$ and $q$ are constants.

Start by completing the square for both $f(x)$ and $g(x)$ ,
$f(x) = x^{2} - 2x + 5$ $f(x) = (x - 1)^{2} + 4$ $g(x) = x^{2} + 4x + 13$ $g(x) = (x + 2)^{2} + 9$ Let’s proceed to the next part,
$g(x) = f(x + p) + q$ Let’s evaluate the equation above. $p$ represents a translation in the x-direction from $f(x)$ to $g(x)$ . To translate from $f(x)$ to $g(x)$ i.e from $-1$ to $2$ , in the x-direction we have to move by $3$ units. Therefore,
$p = 3$ $q$ represents a translation in the y-direction from $f(x)$ to $g(x)$ . To translate from $f(x)$ to $g(x)$ i.e from $4$ to $9$ , in the y-direction we have to move by $5$ units. Therefore,
$q = 5$ Therefore, the final answer is,
$g(x) = f(x + 3) + 5$ (b) Describe fully the transformations which transform the graph of $y = f(x)$ to the graph of $y = g(x)$ .
$g(x) = f(x + 3) + 5$ Start by describing the transformation in the x-axis,
There is a translation in the x-direction by $-3$ units.

Then describe the transformation in the y-axis,
There is a translation in the y-direction by $5$ units.

Therefore, the final answer is,
There is a translation in the x-direction by $-3$ units. Followed by a translation in the y-direction by $5$ units.

GCE_A_Level_Functions__Transformations Download