1.4.1 Circular Measure - GCEALevelMaths9709

In this topic we will learn to:

understand the definition of a radian, and use the relationship between radians and degrees
use the formulae $s = r\theta$ and $A = \frac{1}{2}r^{2}\theta$ in solving problems concerning the arc length and sector area of a circle

$\textbf{\textcolor{gray}{Radian}}$ A radian is an angle whose corresponding arc in a circle is equal to the radius of the circle.

Rendered by QuickLaTeX.com

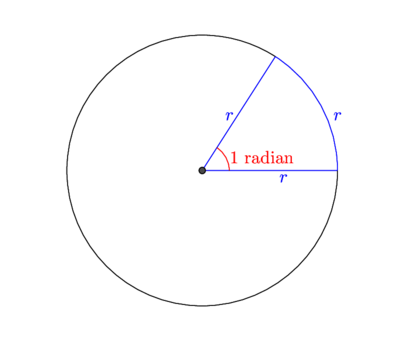
One radian is $\approx 57.2958$ degrees.

To change an angle from radians to degrees, we use the formula,
$\theta = \textmd{angle in radians} \times \frac{180^{\circ}}{\pi}$ To change an angle from degrees to radians, we use the formula,
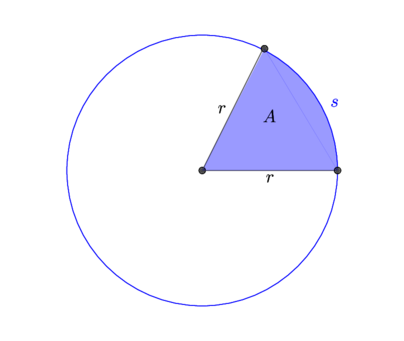
$\theta = \textmd{angle in degrees} \times \frac{\pi}{180^{\circ}}$ $\textbf{\textcolor{gray}{Arc Length}}$ An arc is a portion of the circumference of the circle. The length of that portion is called the arc length. Arc length is represented by the symbol, $s$ . To calculate the arc length, we use the formula,
$s = r\theta$ Where $r$ is the radius of the circle and $\theta$ is the angle of the sector.
$\textbf{\textcolor{gray}{Sector Area of a Circle}}$ A sector of a circle is a pie shaped portion of a circle, consisting of an arc and its two radii. To calculate the sector area of circle, we use the formula,
$A = \frac{1}{2}r^{2}\theta$ Note: The formulae for arc length and sector area of a circle take $\theta$ in radians NOT in degrees.

Let’s look at some past paper questions on this topic.

1. A sector of a circle of radius $r$ cm has an area of $A$ cm $^{2}$ . Express the perimeter of the sector in terms of $r$ and $A$ . (9709/11/M/J/19 number 3)

Rendered by QuickLaTeX.com

Perimeter is the distance around the shape,
$P = r + \textcolor{#2192ff}{s} + r$ Using the formula for arc length, substitute $s$ with $r\theta$ ,
$P = r + \textcolor{#2192ff}{r\theta} + r$ $P = 2r + r\theta$ Use the formula for sector area of a circle, to get rid of $\theta$ ,
$A = \frac{1}{2}r^{2}\theta$ Make $\theta$ the subject of the formula,
$\theta = \frac{2A}{r^{2}}$ Substitute $\theta$ ,
$P = 2r + r\textcolor{#2192ff}{\theta}$ $P = 2r + r\left(\textcolor{#2192ff}{\frac{2A}{r^{2}}}\right)$ Simplify,
$P = 2r + \frac{2A}{r}$ Therefore, the final answer is,
$P = 2r + \frac{2A}{r}$ 2. The diagram shows a sector $ABC$ of a circle with center $A$ and radius $r$ . The line $BD$ is perpendicular to $AC$ . Angle $CAB$ is $\theta$ radians. (9709/11/M/J/22 number 5)

Rendered by QuickLaTeX.com

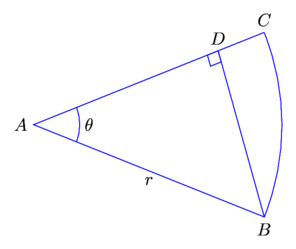
(a) Given that $\theta = \frac{1}{6}\pi$ , find the exact area of $BCD$ in terms of $r$ .

If you look at the diagram, you will notice that the Area of $BCD$ can be written as,
$\textmd{Area of }BCD = \textmd{Area of Sector }ABC -\textmd{ Area of triangle }ABD$ Use the formula for sector area of a circle and area of a triangle,
$\textmd{Area of }BCD = \frac{1}{2}r^{2}\theta - \frac{1}{2} \times BD \times AD$ Substitute in the value of $\theta$ ,
$\textmd{Area of }BCD = \frac{1}{2}r^{2}\left(\frac{1}{6}\pi\right) - \frac{1}{2} \times BD \times AD$ Simplify,
$\textmd{Area of }BCD = \frac{1}{12}\pi r^{2}\theta - \frac{1}{2} \times BD \times AD$ Let’s evaluate $BD$ using Pythagoras,
$\sin{\theta} = \frac{BD}{r}$ $BD = r\sin{\theta}$ Since $\theta = \frac{1}{6}$ , then,
$BD = r\sin\left(\frac{1}{6}\pi\right)$ $BD = \textcolor{#2192ff}{\frac{1}{2}r}$ Let’s evaluate $AD$ using Pythagoras,
$\cos{\theta} = \frac{AD}{r}$ $AD = r\cos{\theta}$ $AD = r\cos\left(\frac{1}{6}\pi\right)$ $AD = \textcolor{#0f0}{\frac{\sqrt{3}}{2}r}$ Let’s substitute $BD$ and $AD$ ,
$\textmd{Area of }BCD = \frac{1}{12}\pi r^{2}\theta - \frac{1}{2} \times \textcolor{#2192ff}{BD} \times \textcolor{#0f0}{AD}$ $\textmd{Area of }BCD = \frac{1}{12}\pi r^{2}\theta - \frac{1}{2} \times \textcolor{#2192ff}{\frac{1}{2}r} \times \textcolor{#0f0}{\frac{\sqrt{3}}{2}r}$ Simplify,
$\textmd{Area of }BCD = \frac{1}{12}\pi r^{2}\theta - \frac{\sqrt{3}}{8}r^{2}$ Therefore, the final answer is,
$\textmd{Area of }BCD = \frac{1}{12}\pi r^{2}\theta - \frac{\sqrt{3}}{8}r^{2}$ (b) Given instead that the length of $BD$ is $\frac{\sqrt{3}}{2}r$ , find the exact perimeter of $BCD$ in terms of $r$ .

Rendered by QuickLaTeX.com

Perimeter is the distance around the shape,
$P = \textcolor{#2192ff}{BD} + CD + arcBC$ Substitute $BD$ with $\frac{\sqrt{3}}{2}r$ ,
$P = \textcolor{#2192ff}{\frac{\sqrt{3}}{2}r} + CD + arcBC$ From the diagram, we can tell that $CD = AC - AD$ ,
$P = \frac{\sqrt{3}}{2}r + \textcolor{#0f0}{(AC - AD)} + arcBC$ From part $(a)$ we know that $AD = r\cos{\theta}$ and $AC$ is the radius,
$P = \frac{\sqrt{3}}{2}r + \textcolor{#0f0}{(r - r\cos{\theta})} + arcBC$ Using the formula for arc length, substitute $arcBC$ with $r\theta$ ,
$P = \frac{\sqrt{3}}{2}r + (r - r\cos{\theta}) + \textcolor{#2192ff}{r\theta}$ We can use Pythagoras to evaluate $\theta$ ,
$\sin{\theta} = \frac{BD}{AB}$ Note: The right-angled triangle allows us to use SOHCATOA.
$\sin{\theta} = \frac{\frac{\sqrt{3}}{2}r}{r}$ $\sin{\theta} = \frac{\sqrt{3}}{2}$ $\theta = \sin^{-1}\left(\frac{\sqrt{3}}{2}\right)$ $\theta = \frac{1}{3}\pi$ Substitute $\theta$ ,
$P = \frac{\sqrt{3}}{2}r + (r - r\cos{\textcolor{#2192ff}{\theta}}) + r\textcolor{#2192ff}{\theta}$ $P = \frac{\sqrt{3}}{2}r + \left(r - r\cos\left(\textcolor{#2192ff}{\frac{1}{3}\pi}\right)\right) + r\left(\textcolor{#2192ff}{\frac{1}{3}\pi}\right)$ Simplify,
$P = \frac{\sqrt{3}}{2}r + \left(\textcolor{#0f0}{r - \frac{1}{2}r}\right) + \frac{1}{3}\pi r$ $P = \frac{\sqrt{3}}{2}r + \textcolor{#0f0}{\frac{1}{2}r} + \frac{1}{3}\pi r$ Therefore, the final answer is,
$P = \frac{\sqrt{3}}{2}r + \frac{1}{2}r + \frac{1}{3}\pi r$ 3. In the diagram, $CXD$ is a semicircle of radius $7$ cm with center $A$ and diameter $CD$ . The straight line $YABX$ is perpendicular to $CD$ , and the arc $CYD$ is part of a circle with center $B$ and radius $8$ cm. Find the total area of the region enclosed by the two arcs. (9709/12/F/M/19 number 3)

Rendered by QuickLaTeX.com

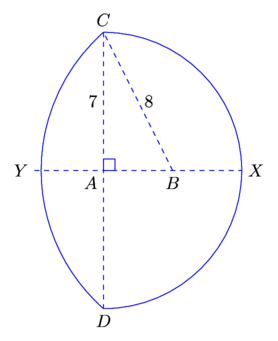
From the diagram, we can tell that the total area can be written as,
$\textmd{Total Area } = \textmd{Area of semicircle }CXD + \textmd{Area of segment }CYD$ Let’s start by finding the Area of semicircle $CXD$ ,
$\textmd{Area of semicircle }CXD = \frac{1}{2}\pi r^{2}$ $CXD$ has a radius of $7$ cm,
$\textmd{Area of semicircle }CXD = \frac{1}{2}\pi (7)^{2}$ Simplify,
$\textmd{Area of semicircle }CXD = \frac{49}{2}\pi$ Let’s find the Area of segment $CYD$ ,
$\textmd{Area of segment } CYD = \textmd{Area of sector }CYD - \textmd{Area of triangle }BCD$ Use formulae for sector area of a circle and area of a triangle,
$\textmd{Area of segment } CYD = \frac{1}{2}r^{2}\theta - \frac{1}{2} \times CD \times AB$ Substitute in $r$ and $CD$ ,
$\textmd{Area of segment } CYD = \frac{1}{2} \times 8^{2} \times \theta - \frac{1}{2} \times 14 \times AB$ Simplify,
$\textmd{Area of segment } CYD = 32\theta - 7\times AB$ Let’s find $AB$ using Pythagoras,
$\textcolor{#2192ff}{a}^{2} + \textcolor{#0f0}{b}^{2} = \textcolor{red}{c}^{2}$ $(\textcolor{#2192ff}{AB})^{2} + (\textcolor{#0f0}{AC})^{2} = (\textcolor{red}{BC})^{2}$ $(AB)^{2} + 7^{2} = 8^{2}$ $(AB)^{2} = 8^{2} - 7^{2}$ $(AB)^{2} = 15$ $AB = \sqrt{15}$ Substitute $AB$ and simplify,
$\textmd{Area of segment } CYD = 32\theta - 7\times \textcolor{#2192ff}{AB}$ $\textmd{Area of segment } CYD = 32\theta - 7\times \textcolor{#2192ff}{\sqrt{15}}$ $\textmd{Area of segment } CYD = 32\theta - 7\sqrt{15}$ Let’s find $\theta$ ,
$\theta = 2ABC$ $\sin(ABC) = \frac{AC}{BC}$ $\sin(ABC) = \frac{7}{8}$ $ABC = \sin^{-1}\left(\frac{7}{8}\right)$ $\theta = 2\sin^{-1}\left(\frac{7}{8}\right)$ Substitute $\theta$ and simplify,
$\textmd{Area of segment } CYD = 32\textcolor{#2192ff}{\theta} - 7\sqrt{15}$ $\textmd{Area of segment } CYD = 32\left(\textcolor{#2192ff}{2\sin^{-1}\left(\frac{7}{8}\right)}\right) - 7\sqrt{15}$ $\textmd{Area of segment } CYD = 64\sin^{-1}\left(\frac{7}{8}\right) - 7\sqrt{15}$ Therefore, the total area is,
$\textmd{Total Area } = \textcolor{#2192ff}{\textmd{Area of semicircle }CXD} + \textcolor{#0f0}{\textmd{Area of segment }CYD}$ $\textmd{Total Area }= \textcolor{#2192ff}{\frac{49}{2}\pi} + \textcolor{#0f0}{64\sin^{-1}\left(\frac{7}{8}\right) - 7\sqrt{15}}$ $\textmd{Total Area }= 118.0$ Note: Remember that $\theta$ is in radians, so evaluate any trig functions in radians.

Therefore, the final answer is,
$\textmd{Total Area }= 118.0$

GCE_AS_Level_Circular_Measure Download